任政勇

基于四面体网格的三维大地电磁反演体系

1.1  起伏地形情况下三维大地电磁自适应反演

当前，三维大地电磁反演常采用固定反演网格。过稀的反演网格无法逼近复杂的地下电导率分布,还可能导致反演结果无法收敛而过密的反演网格不仅将加大反演的计算成本，还会增加反演的非唯一性。针对上述问题，本文提出了一种基于灵敏度矩阵和模型梯度共同驱动的三维大地电磁自适应反演策略，以实现反演网格的自适应调整。首先，基于非结构化有限元技术实现了对任意复杂带地形三维地电模型的精确正演；其次，生成嵌套的正、反演四面体网格，实现了正反演网格的解耦；建立基于光滑约束的Thikhonov正则化目标函数，采用L-BFGS最优化算法、基于伴随原理的目标函数梯度求解策略以及正则化因子“冷却”技术实现了对目标函数的最优化求解。然后，提出了一种基于灵敏度矩阵和模型梯度双重约束的反演网格调整策略，实现了最优化过程中的反演网格自适应调整。最后，通过对多个理论模型的合成数据和实测数据的反演验证了该自适应反演算法的可靠性、稳定性和实用性。

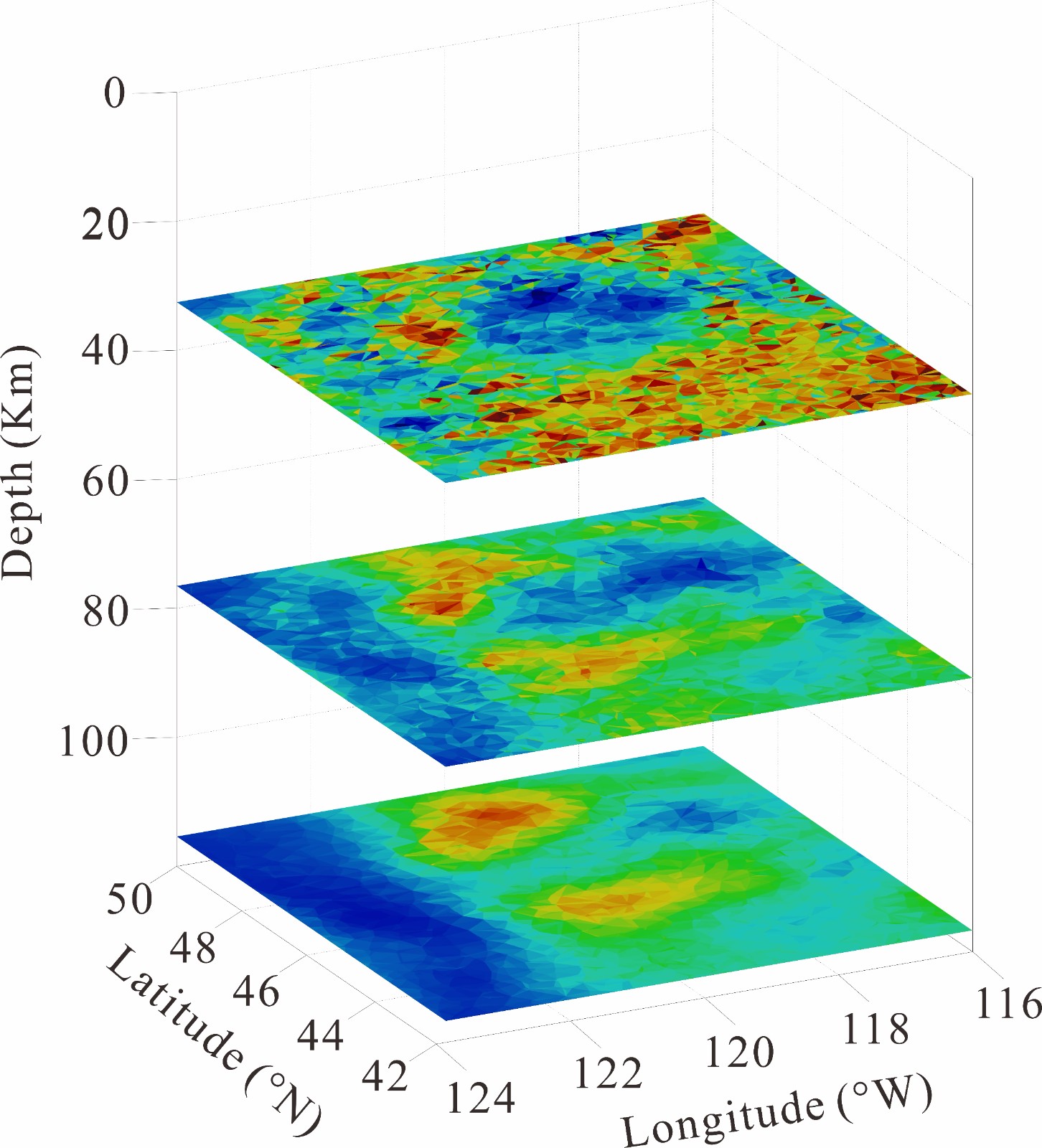
(Huang Chen, Zhengyong Ren*, Jingtian Tang, et.al. JGR-solid earth, 2022, under preparing.)

1.2 基于地质与地球物理信息的大地电磁三维约束反演

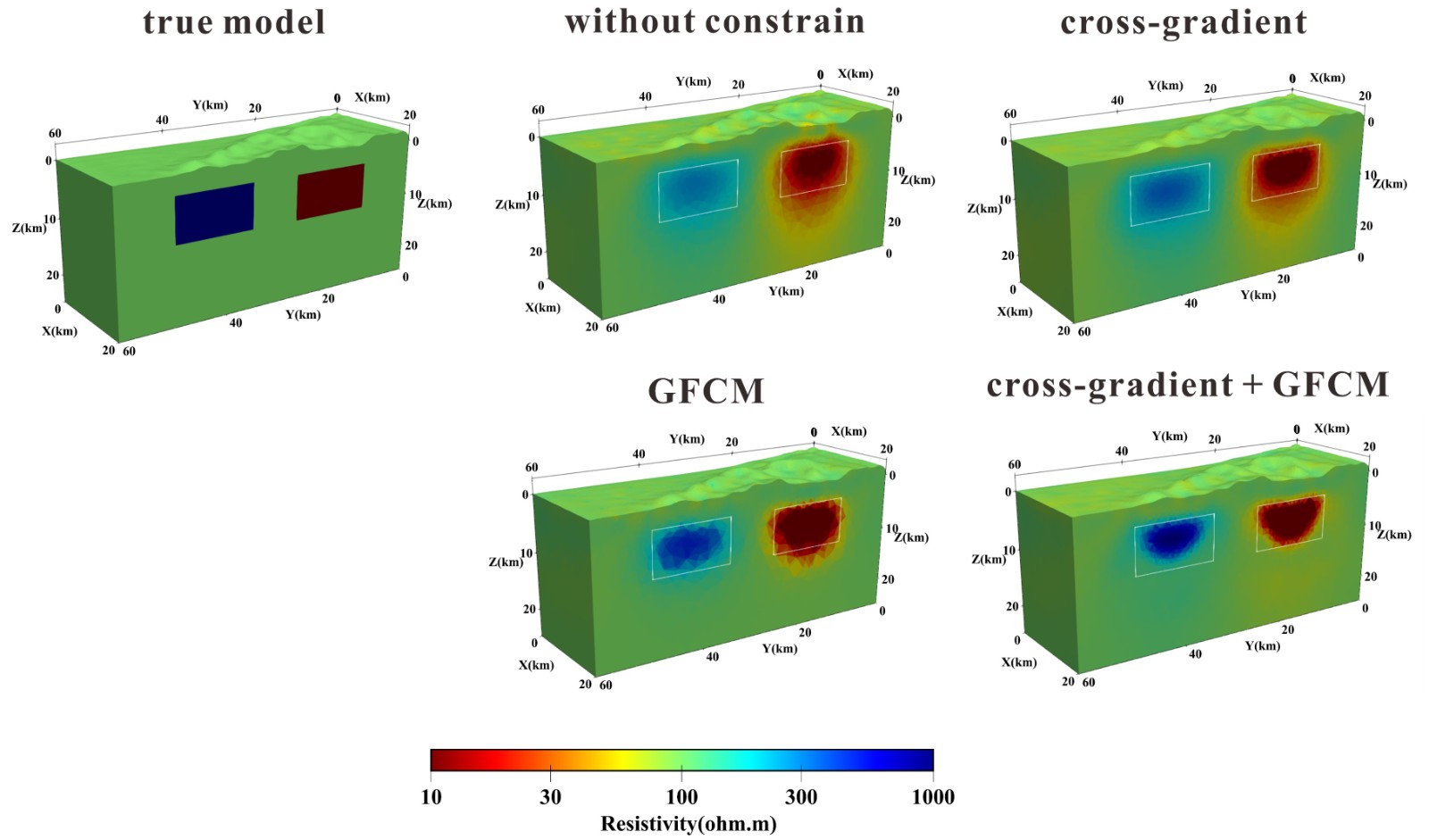
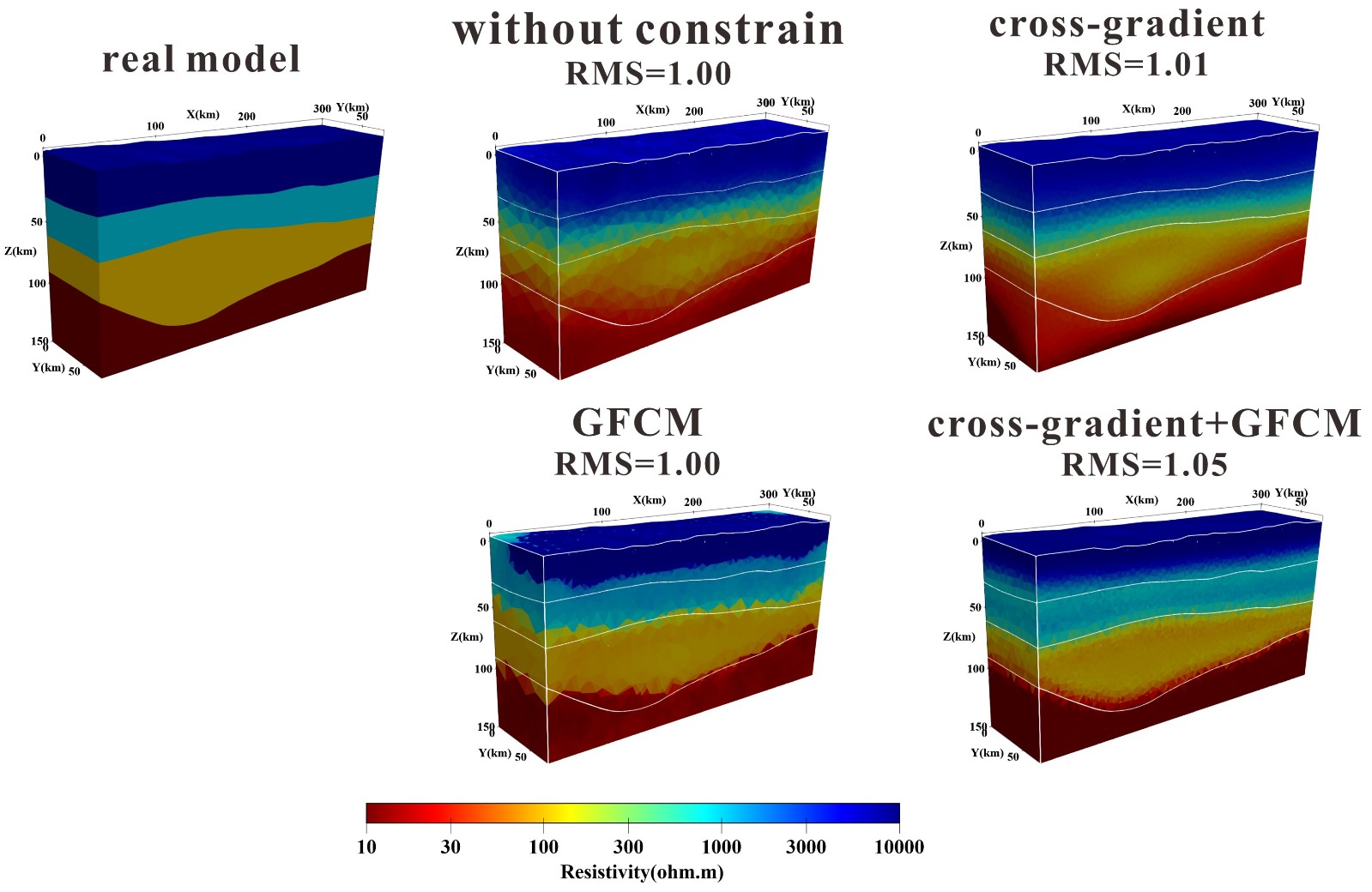
由于观测数据的有限性与噪声的影响，大地电磁数据的三维反演往往存在严重的多解性，严重影响地质解释的可靠性。为了降低反演的多解性，得到更可靠的结果，有必要在反演过程中添加先验地质与地球物理信息，对大地电磁数据进行约束反演。

本文开发了一个三维大地电磁数据约束反演的框架，该框架能够根据先验信息使用交叉梯度和GFCM约束方法约束反演过程。网格使用了非结构化四面体网格，反演算法使用了高斯牛顿方法对目标函数进行最优化。我们首先使用两个理论模型验证了约束反演算法的可靠性，然后将约束反演算法应用于铜陵的大地电磁数据。得到的结果表明，本文的约束反演算法能够有效提升反演结果的可靠性与分辨率。